昨日我們介紹了因數分解機(FM)的特色，今天我們來說明它為什麼有用！

推薦問題在線性回歸上是怎麼運作的？

在做推薦系統時，若用線性回歸做預測，要預測的東西會有 2 種：

1. 預測分類：要推薦或不推薦
2. 預測數字：預測使用者對這電影的評分。

無論哪一種，若 x 是特徵向量，那要預測的值為 y(x) ，則 y 就是單純的數字，不是向量。

若特徵向量 x 是 n 維的，則 y(x) 計算方式如下：

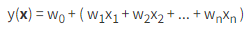
這式子用直覺來說明：

1. y 的值是由一個基準值 w0 開始。
2. 針對特徵向量裡的每個維度 i 給一個權重 wi，若這維度對於 y 的影響大的話， wi 數字就大，若是正相關就是正數，若負相關就是負數。

所以傳統的線性回歸，可以視為如何調整基準值 w0 及每個維度權重 w1 ~ wn 的問題，共有 n + 1 個權重要調整的問題。

因為 上面的式子可微分，所以可以使用梯度下降法 SGD，來找出所有的權重（共n + 1 個），來逼近我們想要的結果。

這樣不夠！特徵的運用還可以更多一些

但是想想這樣不夠，我們對於特徵的運用，還可以更多一些。

舉個例子，人若要減肥，其中「脂肪」和「澱粉」的攝取變得很重要。但單純「脂肪」或「澱粉」攝取量對增重或減重的影響，也許就一般般；也就是說，如果單純吃飯或單純喝油，可能都胖不快。這就像是線性回歸算法裡的一階的權重，一個個討論，影響都不大。

但如果「脂肪」和「澱粉」一起出現，就變成必肥配方。例如正常吃飯胖不了多少，但用正常飯量吃了滷肉飯就必肥！

也就是說，我們在做預測時，如果可以把兩個特徵同時出現考慮進來，並給他一個權重，那我們的算法就變成了：除了考慮一個個特徵對結果的影響外，還考慮了兩個特徵同時出現時對結果的影響！

換到電影推薦來說，也許有人對於愛情片的感覺還好，對於有外星人影片也感覺還好，但有愛情加的外星人片就變得超喜歡，這時系統就可以推來自星星的你...大概就是這個意思。

兩個特徵同時出現的式子是什麼樣子呢？

為了要多了計算2個特徵同時出現時對結果的影響，所以 y(x) 式子就寫成：

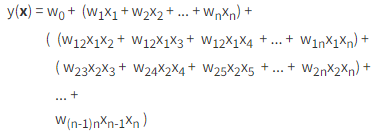
其中 w12x1x2 可以視為當 x1 和 x2 同時出現時，我們給它一個 w12 的權重來表達這兩特徵同時出現時對結果 y 的影響。

因為是要描述 x1 和 x2 同時出現，所以不需要加入 w21x2x1 這樣的計算進來。也不需要加入 w11x1x1 這樣的項進到式子裡。

到這個程度，我們的問題就變成如何調整以下 3 類權重問題了

1. w0 , 1 個
2. 1 階權重 w1 ~ wn 共n個
3. 2 階權重 共 (((n-1)+1) * (n-1))/2 = n(n-1)/2 個

所以變成 1 + n + n(n-1)/2 個參數調整問題。

接下來呢？

雖然上面的式子已把2個特徵同時出現的事情放進了 y 的計算式裡，但要調整的參數也太多了！並且權重的數目算式裡，還有個平方在！當 n 大起來的時候，計算量機器會 hold 不住呀！怎麼辦呢？

這大運算量問題被 FM 演算法給解決了，這算是 FM 的精華了，至於怎麼做，這個我們明天再和大家分享！